4. Natural Notes
Don't B Sharp, Don't B Flat, Just B Natural

Natural means to forget about sharping or flatting a letter or note, just play it normally (naturally). The B we are playing stays a B. The F we are playing stays an F. The same goes for every music letter or note.
5. What Do Half Steps SOUND Like?

james taylor & carole king
We know the difference between a higher and a lower sound. But how much higher is going up a half step(#), or how much lower is going down a half step(b)?
- On a guitar, only one fret up is a half step.

- On a piano, one half step up is the next key to the right (including black keys).

- On a flute, a half step is as simple as removing a finger from a key. The opposite is true of a half step down, such as one fret, or one key down.

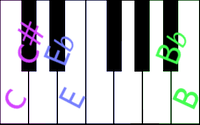
For a half step up: A to A# is the (guitar) fret between A and B. So, we hear that there isn't much difference in sound between a half step up (#) or a half step down(b).
B to Bb is the next (piano) key going down from B natural. The half step is relative to the natural note's name it goes up(#) from, or down(b) to, landing a half step from the natural note (like natural C to C#, or natural E to Eb).
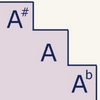
Furthermore, to flat a note that's already sharped, and vice versa, make the note natural, since we're stepping up or down to the note. These half steps are like stairs. They raise or lower a natural note's sound.
6.The G and A Connection
What happens after we reach G? Return to the letter A. Is there a step between G and A?
Yes. Between B and C, and between E and F (Bake Cakes, Eat Food), are the only exceptions where there are no between steps. The remaining letters have steps between:
Naturals to Sharp or Flat
Steps are either flat from the natural note above, or sharp from the natural note below:
I'll refer to these letters as notes we can hear. Again, if the step between is flat, it takes on the higher natural note's letter (B to Bb going down). If the step is sharp, it takes on the lower natural note's letter (A to A# going up).
This is logical, because a sharped note SOUNDS higher than the previous note. Likewise when we flat a note, the note SOUNDS a half step lower from the note we flatted (B to Bb).
To simplify: One key up from A on the piano is A#. One key down from B is Bb. Notice that A# and Bb are the same note. We call this kind of note an Enharmonic, explained soon.
Before, we labelled the placeholder between natural notes as 'steps'. Let's now view it as a half step before the sharp or flat note, and another half step after the sharp or flat note. That makes a whole step between the natural notes (except bc,ef):
- CstepC#stepD =whole step; DstepDbstepC =whole step
7. Scales

gregory hines & luther vandross
Scales are important, because they use notes in a way that sound pleasant to the ear. There are many different types of Scales, but our focus is the Major Scale.
It's the type of scale that is used in most music today, and sounds like the musical phrase, 'Do Re Mi Fa So La Ti Do'. We would have a Major Scale, if we were to play:
Notice how the scale ascends the letters of the alphabet, ending on the same note it started, with 8 letters total. However, should we start with a different alphabet letter, not all of the notes would be played in their natural state; some scale notes would either be sharp#, or flatb.
In fact, some Major scale notes are between the natural notes, making them sharp or flat. This is because of the sound. We want all Major Scales to have the same basic sound pattern, no matter on which note we start. The starting note (root) will not sound the same for different Major scales, but the basic, overall sound pattern of the whole Major Scale is the same. We space out the notes in a certain pattern we'll see next.
Major Scale Steps
We remember a sharp and flat are half steps up or down, from a note. And two half steps added together makes a whole step between two notes.
To explain these Major Scale steps better, start with the letter A:
Since we want a specific sound, we change particular notes. Here, B to C is a half step, and C to C# is another half step, making a whole step between B - C#. The full scale step pattern has 2wholes, 1 half, 3wholes, then 1half steps:
This pattern of steps works for every letter on which we may start a Major Scale. It makes a phrase of sound (scale) from any note we start. We can play it backward or forward, starting and ending on the same note.
Here's the A Major Scale, with the steps removed:
Why is there a whole step between only some of the letters? To explain, A to A# is a half step, and A# to B is another half step. So, add those two half steps together to make a whole step from A to B, in our scale above:
A h A# h B
Again, F# to G is a half step, and G to G# is a half step. So, F# to G# is a whole step:
F#h G h G#
It is easier to play the steps on an instrument, so we may both see and hear this scale pattern.
We organize our notes into sound patterns through note distances, whole or half steps. These change, but still use the letters A-G.
The page, Sharp Flat Rule has more on Major scales.
8.Enharmonics
Interestingly, two different names may denote one Sharp or Flat step between two notes. Different names, but the same sound: A (A# and Bb) B or, G (G# and Ab) A
The notes A# and Bb are the same note, and G# and Ab are the same note:
A# = Bb , G# = Ab

stevie wonder
While these between steps have two different names, one sharp and one flat, each tone is the same. It is the same sound, because both refer to one note. This note with two different names, but one sound, is called an Enharmonic.
An enharmonic has two different names, relative to whether the melody uses sharps or flats for its key. The key of a song will determine which enharmonic sharp or flat note appears.
Use two consecutive notes to sharp or flat them to find the enharmonic between them. And, the enharmonic's name isn't as important as its sound.
Now we may say there are two (half) steps between consecutive notes. Because from one note to the flat or sharp tone is a half step, and from the flat or sharp tone to the next note is a half step:
D to D#, then D# to E are two half steps, going up. Likewise, going down, E to Eb, then Eb to D:
D h D# h E
E h Eb h D
D# = Eb
To be thorough, scales going up may also have flats, such as the Eb major scale:
Again, we change the name of this enharmonic tone to match the scale or key we're playing in, sharp or flat.
9. Chromatics
Chromatics is just a fancy term for all half steps, either up or down:
C C# D D# E F F# G G# A A# B C (for sharps)
descending: G Gb F E Eb D Db C B Bb A Ab G (for flats)
Both of these are examples of a chromatic scale. Music uses half steps for sounding sad (down), or excited (up).
Chromatics have only half steps, differing from Major Scales that have both half and whole steps.
Additionally, Chromatics smoothly transition between scales and phrases within a melody. This is due to chromatic graduations, or half step intervals. Basically, an instrument's frets, keys, or vocal leaps may allow an easy chromatic rise or fall into another scale or phrase. Half steps, up or down, are small note changes to quickly find another scale.
Seeing all the notes available, music simply scrambles their order to get different sounds (and rhythms). Theory explains these new patterns.
The next page changes a scale's first note to form keys, through a combination of half and whole steps.